
Email: phyfeng@nus.edu.sg
Current Research
Dr Feng Ling specializes in complex systems research, both in theoretical foundations and practical problems, ranging from the statistical physics behind deep learning to social systems. In his theoretical studies, he looks at the complexity and phase transition phenomena in artificial neural networks, trying to uncover the working principle of deep learning. He has also been working on the various percolation transition phenomenon in inter-dependent complex networks to develop frameworks to construct different phases in spreading phenomena. In the application of complexity theories, he has applied complex network theories to various social and economic networks ranging from social media, financial networks and blockchain networks, building predictive algorithms in synergy with various machine learning algorithms.
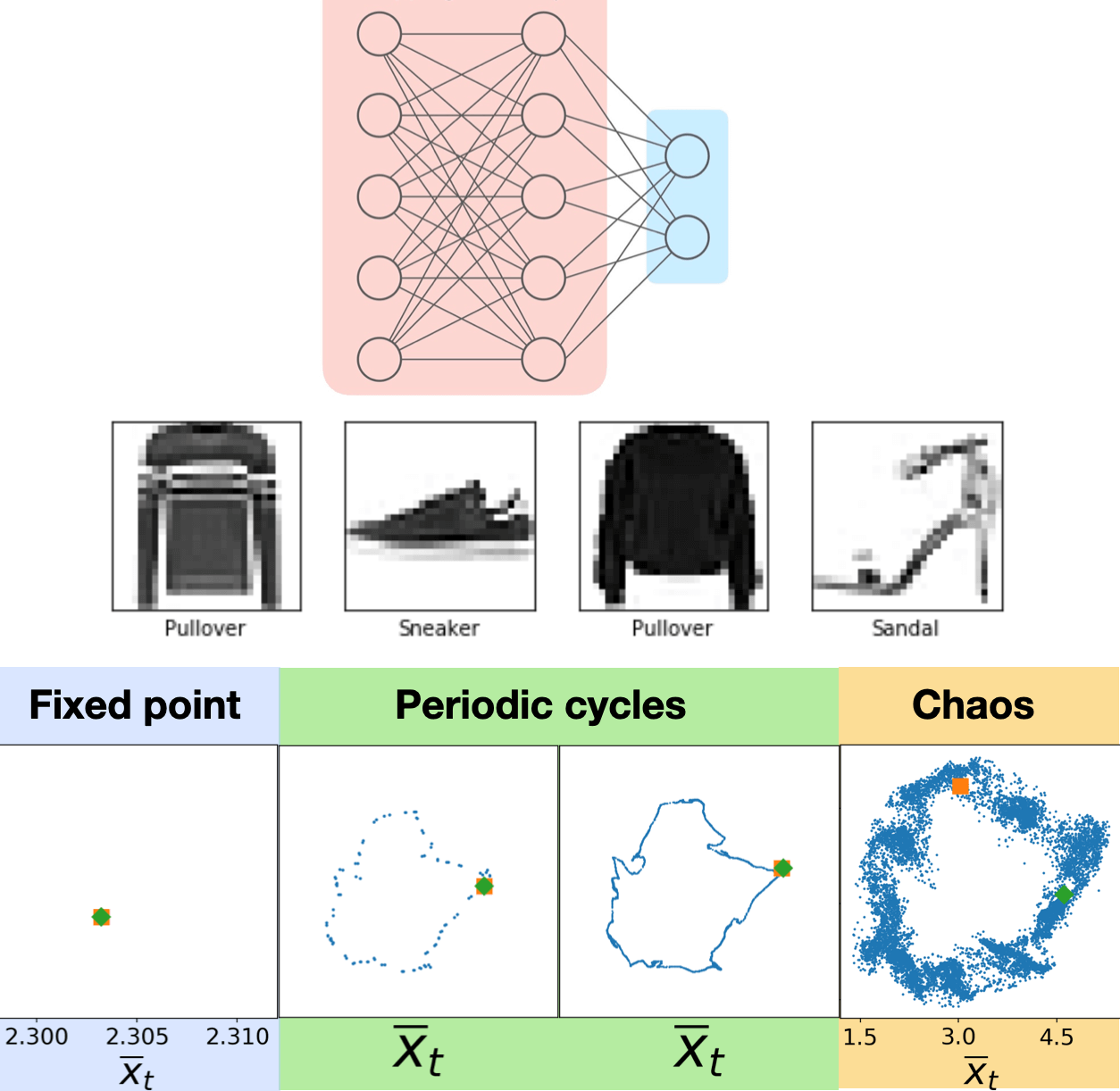
- Order to chaos phase transition during the training of deep neural networks on Fashion MNIST dataset, with the optimal performance at the transition between periodic cycles and chaos.
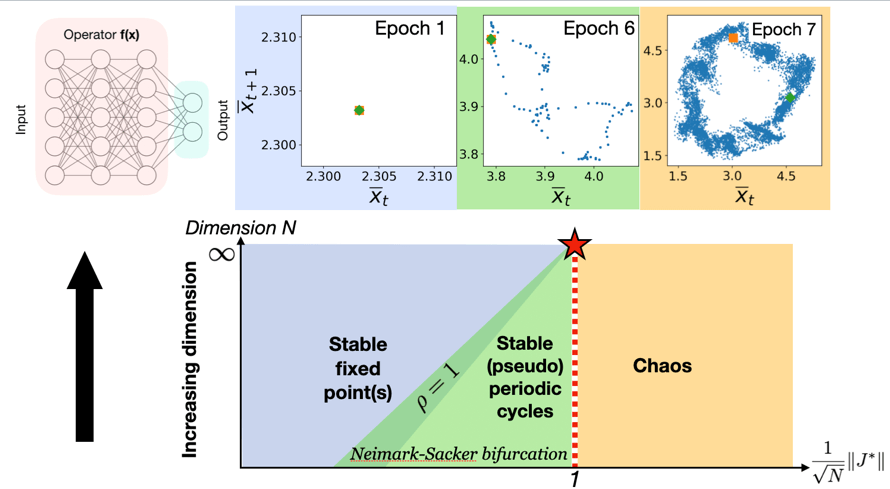
- Complexity science of deep learning. Biological brains have been found to work near some critical state, and some studies have demonstrated through simulations that certain critical state possess the ability to transfer high amount of information. By examining the modern deep neural networks, we have uncovered the theoretical principle behind this phenomenon, and further pinpointed the critical state to be between periodic cycles and chaos, universal across different dynamical systems. Such finding leads to new potential avenues to design and train neural networks, as well as extracting their explainability.
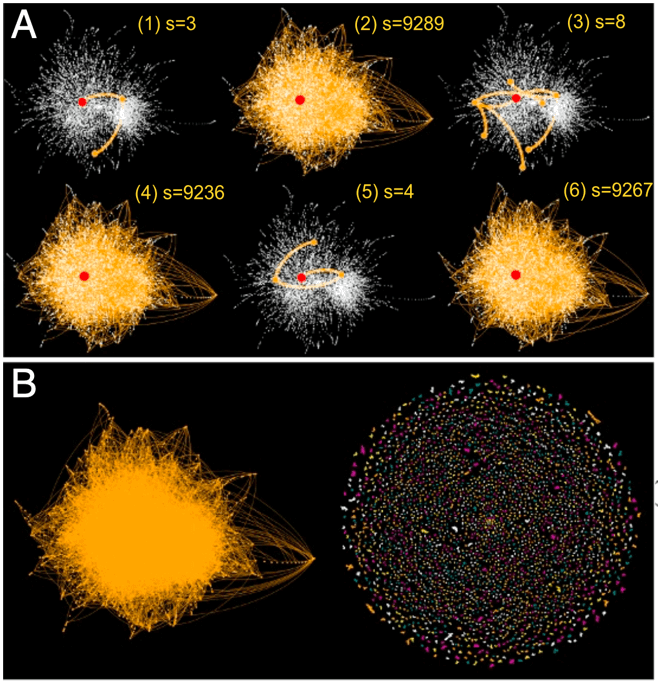
- Percolation in complex networks. Many real world systems can be represented as networks, over which interactions occur. Such systems usually, if not always exhibits phase transition behaviors like the melting of ice to water. One thing in common in many of such systems are the spreading events, ranging from infectious disease over human contact network to information over online social media. Typically there are two distinct phases of the spreading outcomes: limited local spread vs. global widespread. In different problems, the desirable phase can be the former or the later. Through percolation theory in statistical mechanics, we have developed frameworks and tools to understand and quantify such phase transitions in various social economic systems, and developed various algorithms to efficiently maximize or mitigate spreading at the systemic level.
Selected Publications
- Chong, Nicholas Jia Le, and Ling Feng. “Self-organization toward 1/f noise in deep neural networks.” Chaos: An Interdisciplinary Journal of Nonlinear Science 34.8 (2024).
- Wang, Junya, et al. “Reconstructing the evolution history of networked complex systems.” Nature Communications 15.1 (2024): 2849.
- Zhang, L., Feng, L.*, Chen, K., & Lai, C. H. (2024). Asymptotic Edge of Chaos as Guiding Principle for Neural Network Training. International Journal of Artificial Intelligence and Robotics Research, 1(01), 2350001.
- Zhang, Lin, Li Shaohua and Feng, Ling, “Predicting Generalization in Deep Learning” Competition at NeurIPS 2020, Technical workshop, 9th place in Competition: https://sites.google.com/view/pgdl2020.
- Feng, L., Zhang, L. and Lai, C.H., “Optimal machine intelligence near the edge of chaos”, arXiv:1909.05176, 2020
- Sun, J., Feng, L., Xie, J., Ma, X., Wang, D., & Hu, Y. (2020). Revealing the predictability of intrinsic structure in complex networks. Nature communications, 11(1), 574.
- Xie, J., Wang, X., Feng, L., Zhao, J. H., Liu, W., Moreno, Y., & Hu, Y. (2022). Indirect influence in social networks as an induced percolation phenomenon. Proceedings of the National Academy of Sciences, 119(9), e2100151119.
- Ma, Sijuan, Ling Feng*, and Choy-Heng Lai. “Mechanistic modelling of viral spreading on empirical social network and popularity prediction.” Scientific reports 8.1 (2018): 13126.
- Hu, Yanqing, et al. “Local structure can identify and quantify influential global spreaders in large scale social networks.” Proceedings of the National Academy of Sciences 115.29 (2018): 7468-7472.
Affiliations & Links
- Manager of Complex System Group, Institute of High Performance Computing, A*STAR
